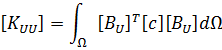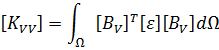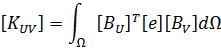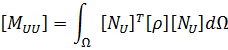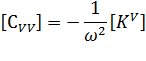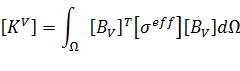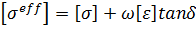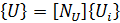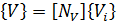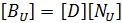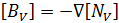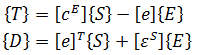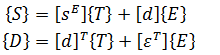Расчет ультразвуковых датчиков
Выполняемые расчеты
Если у Вас есть параметры материалов и геометрия пьезоэлектрического преобразователя, по согласованию с Инженерными решениями, возможно заказать рассчет параметров пьезоэлектрического преобразователя. Мы можем выполнить следующие виды работ:
Гармонический анализ
- расчет амплитудно-частотных характеристик (АЧХ) и фазо-частотных характеристик (ФЧХ) проводимости и импеданса преобразователя / пьезоэлемента;
- расчет АЧХ и ФЧХ чувствительности пьезоэлектрического преобразователя;
- расчет АЧХ и ФЧХ усредненных амплитуд перемещений излучающей поверхности пьезоэлектрического преобразователя;
- определение формы колебаний преобразователя на интересующей частоте.
-
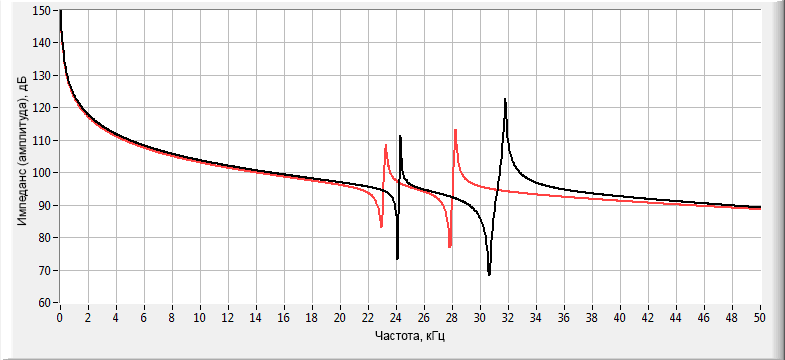
![Сравнение АЧХ импеданса пьезоэлектрических преобразователей Сравнение АЧХ импеданса пьезоэлектрических преобразователей]()
Пример сравнения АЧХ импеданса двух разных вариантов моделей пьезоэлектрических преобразователей -
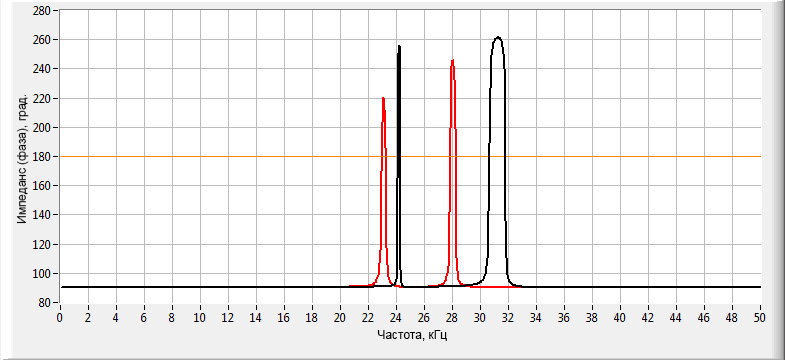
![Сравнени ФЧХ импеданса пьезоэлектрических преобразователей Сравнени ФЧХ импеданса пьезоэлектрических преобразователей]()
Пример сравнения ФЧХ импеданса двух разных вариантов моделей пьезоэлектрических преобразователей
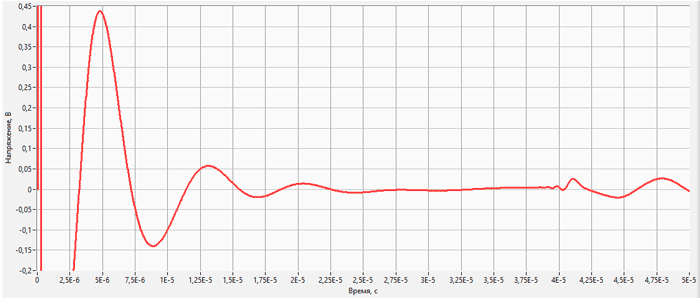
Анализ переходных процессов
- расчет осциллограмм напряжения на пьезоэлементе;
- расчет перемещений излучающей поверхности.
У нас также есть база материалов, состоящая более чем из 100 компонентов, включая металлы, полимеры, композиты, пьезокерамические материалы (ЦТС-19 и ЦТС-26) и др.
Уравнения конечных элементов для пьезоэлектрического анализа
Аллик и Хьюз разработали метод конечных элементов для пьезоэлектрических материалов в 1970 [1]. Для анализа методом конечных элементов ANSYS использует следующую форму уравнений: [4]
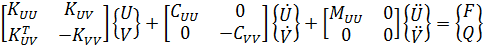
-
- где {U} - вектор перемещений элемента,
- {V} - вектор узловых потенциалов,
- [KUU] - матрица жесткостей элемента,
- [KVV] - матрица коэффициентов диэлектрической проницаемости элемента,
- [KUV] - матрица пьезоэлектрических коэффициентов элемента,
-
- [CUU] - матрица механического (структурного) демпфирования элемента,
- [CVV] - матрица диэлектрических потерь элемента,
- [MUU] - матрица масс элемента,
- {F} - вектор узловых и поверхностных сил,
- {Q} - вектор отрицтельного электрического заряда.
здесь [3]
-
- где c - жесткость, Н/м2,
- ε - диэлектрическая проницаемость, Ф/м, [2]
- e - пьезоэлектрический коэффициент механического напряжения, Кл/м2,
- ρ - плотность, кг/м3,
- σ - электрическая проводимость, См/м,
- tanδ - тангенс угла электрических потерь,
- ω - угловая частота, рад/с
- Ω - объем, м3,
-
- [KV] - матрица коэффициентов электропроводности элемента,
- [σeff] - матрица "эффективной" проводимости,
- [NU] - функции формы конечного элемента,
- [BU] - матрица деформаций (растяжений) -перемещений,
- [BV] - матрица электрических потенциалов - напряженностей электрического поля
Поля перемещений {U} и электрических потенциалов {V} в конечном элементе могут быть определены в терминах узловых перемещений {Ui} и узловых электрических потенциалов {Vi} с помощью соответствующих функций формы, определенных как [NU] и [NV]:
Векторы деформаций {S} и электрических полей {E} связаны с полем перемещений {U} и электрических потенциалов {V} следующими уравнениями соответственно:
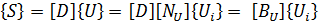
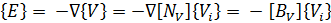
Здесь [D] это дифференциальный оператор определенный как:
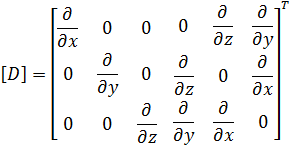
- Henno Allik, Thomas J. R. Hughes. Finite element method for piezoelectric vibration.- Groton, Connecticut, USA.: General Dynamics, Electric Boat Division, 1970
- Florence Rosenblatt-Weinberg. Modelling and optimisation of Electro-Active Polymer (EAP) devices.- London.: Imperial College of Science, Technology and Medicine, 2013
- Vinh-Tan Nguyen, Pankaj Kumar and Jason Yu Chuan Leong. Finite Element Modellingand Simulations of Piezoelectric Actuators Responses with Uncertainty Quantification.- Singapore.: Institute of High Performance Computing, 2018
- ANSYS Help. Theory reference. Piezoelectrics.
Библиографический список
Различия в представлении параметров пьезоэлектрических материалов IEEE и ANSYS
В линейном пьезоэлектричестве уравнения линейной упругости (механика твердого тела) связаны с уравнением заряда (электростатика) с помощью пьезоэлектрических постоянных (стандарт IEEE по пьезоэлектричеству):
-
Уравнения ANSYS
(форма механическое напряжение - заряд)![]()
- где {T} - 6x1 вектор механического напряжения (порядок компонентов x, y, z, xy, yz, xz), Н/м2
- {S} - 6x1 вектор относительной деформации (порядок компонентов x, y, z, xy, yz, xz), м/м
- {D} - 3x1 вектор электрической индукции (порядок компонентов x, y, z), Кл/м2
- {E} - 3x1 вектор напряженности электрического поля (порядок компонентов x, y, z), В/м (Кл/Н)
- [cE] - 6x6 матрица жесткости, определенная при постоянном электрическом поле, Н/м2
- [e] - 6x3 пьезоэлектрическая матрица, связывающая механическое напряжение и электрическое поле, Кл/м2 или Н/Вм
- [e]T - транспонированная матрица [e]
- [εS] - диэлектрическая матрица определенная при постоянной деформации, Ф/м
-
Уравнения производителей пьезокерамики
(форма деформация - заряд)![]()
- где {T} - 6x1 вектор механического напряжения (порядок компонентов x, y, z, yz, xz, xy), Н/м2
- {S} - 6x1 вектор относительной деформации (порядок компонентов x, y, z, yz, xz, xy), м/м
- {D} - 3x1 вектор электрической индукции (порядок компонентов x, y, z), Кл/м2
- {E} - 3x1 вектор напряженности электрического поля (порядок компонентов x, y, z), В/м (Кл/Н)
- [sE] - 6x6 матрица поддатливости, определенная при постоянном электрическом поле, м2/Н
- [d] - 6x3 пьезоэлектрическая матрица, связывающая деформацию и электрическое поле, Кл/Н
- [d]T - транспонированная матрица [d]
- [εT] - диэлектрическая матрица определенная при постоянном механическом напряжении, Ф/м
IEEE и ANSYS используют разное матричное представление.
Моделирование пьезопреобразователей
- Моделирование физических процессов позволяет с большой точностью (погрешность не больше 5%) рассчитать характеристики датчика и его выходные параметры, например такие как:
- амплитуда колебаний (перемещения);
- резонансные частоты;
- напряжение на пьезоэлементе и др.
Таким образом разработчик может быть более гибким на концептуальной стадии проектирования. И только после вычисления оптимальной конструкции датчика изготовить опытные образцы и провести опытные испытания. Это дает возможность значительно снизить затраты на этапе разработки и заранее предвидеть подводные камни.
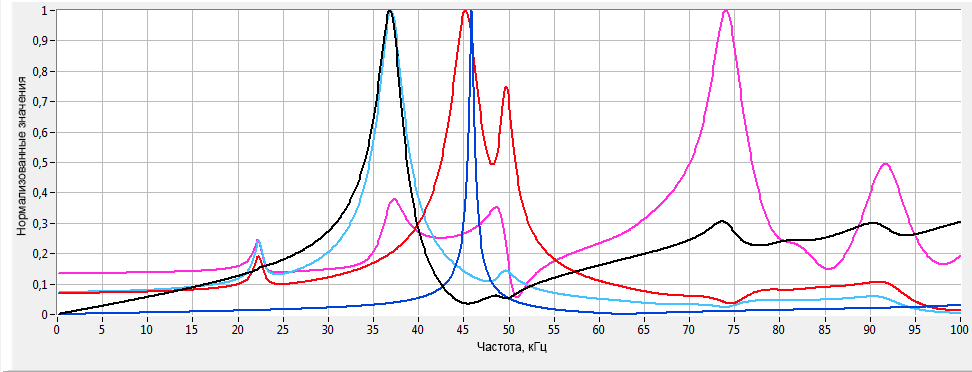
Расчет пьезоэлемента
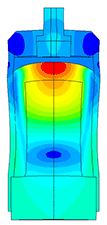
Самым сложным в расчете ультразвуковых пьезодатчиков является моделирование пьезоэлемента. Для правильного расчета пьезоэлектрического элемента требуется знать большое количество параметров пьезокерамики. На графике (рисунок 1) представлено АЧХ пьезоэлемента снятое экспериментально с помощью АЧХометра и расчетное АЧХ пьезоэлемента. Погрешность по частоте составляет 2,3 % (на первом резонансе) и 0,34 % (на втором резонансе).
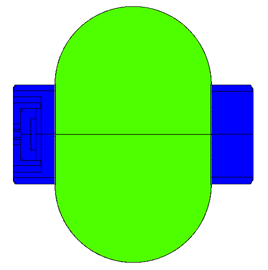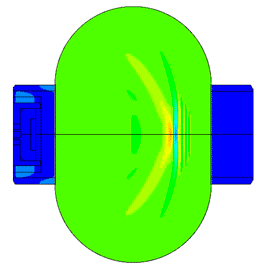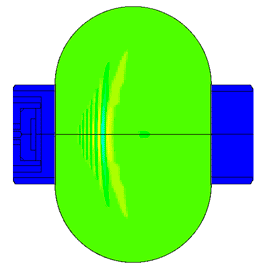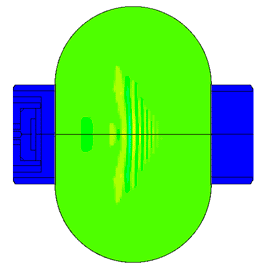
Масштаб колебаний 200000:1
Масштаб колебаний 10000:1


Масштаб колебаний 10000:1
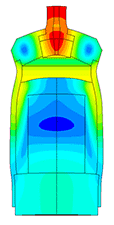
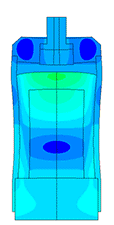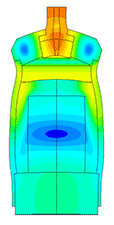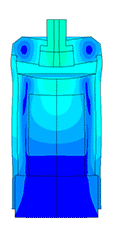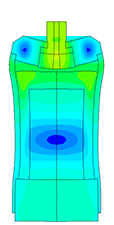
Датчик толщины льда
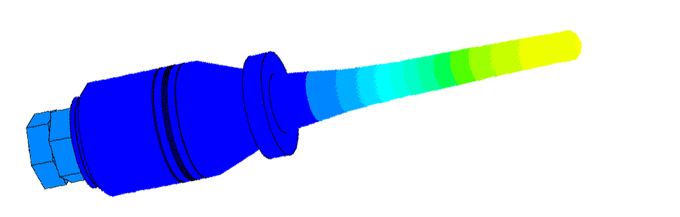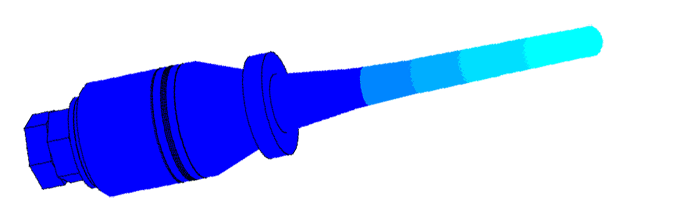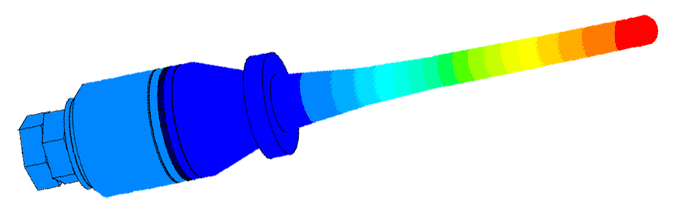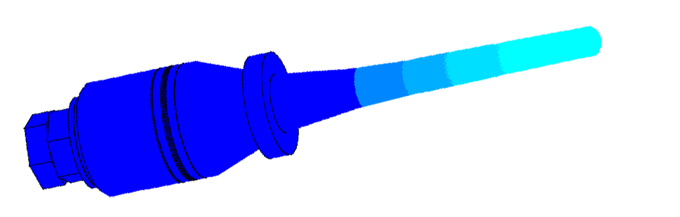
Масштаб колебаний 10000:1
- В задачу входило:
- расчет резонансной частоты;
- определение зависимости частоты от количества льда;
- расчет паразитных колебаний в месте крепления;
- определение области чувствительности датчика.
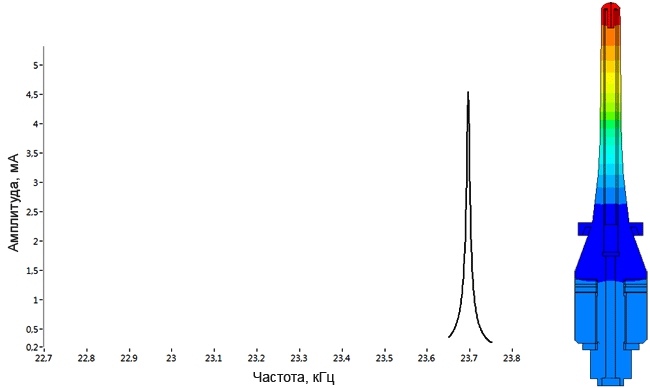
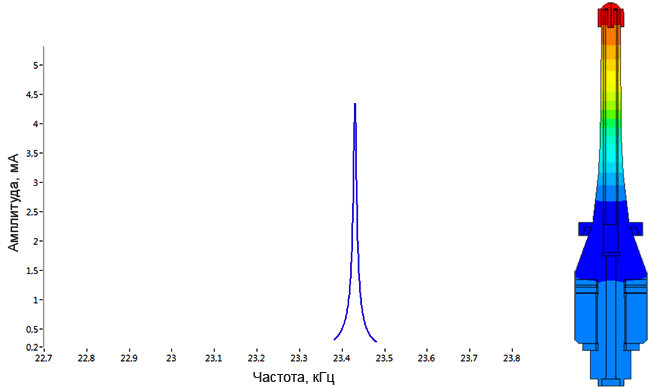
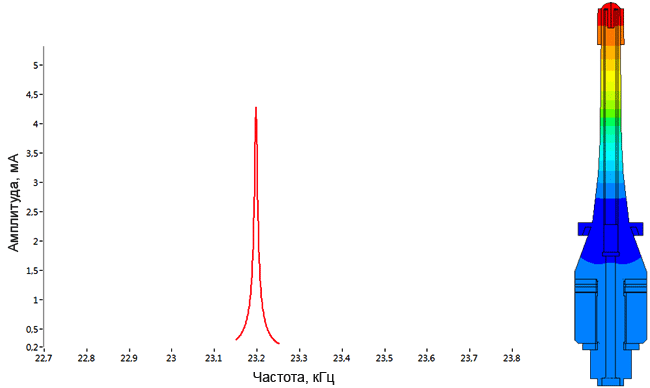
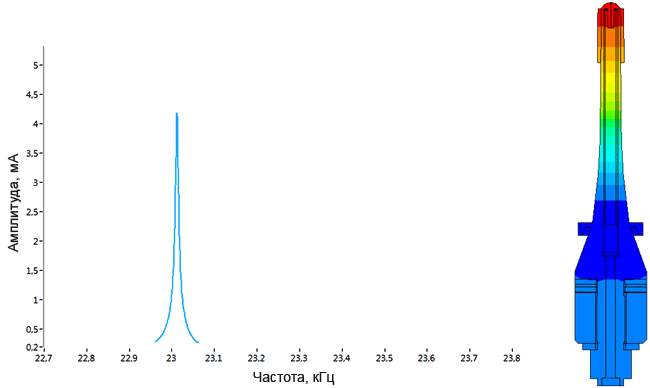
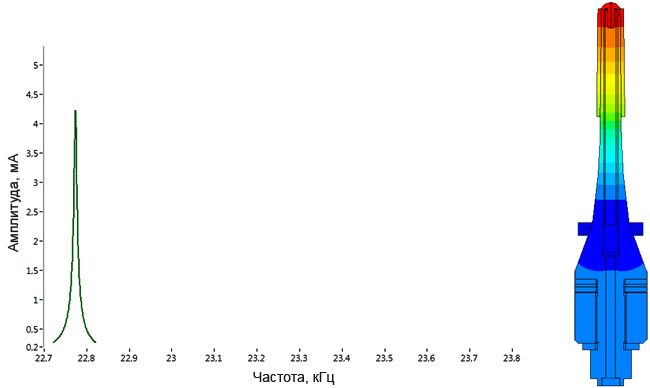
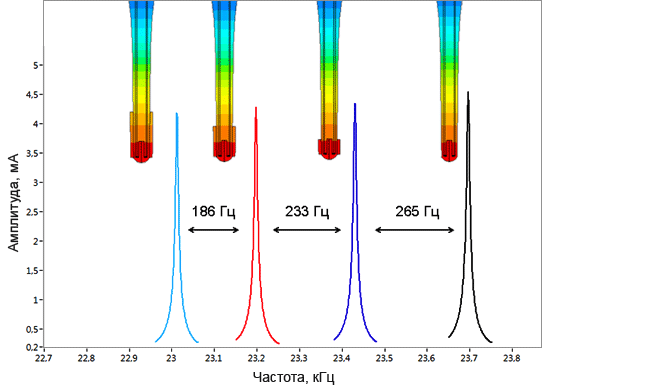
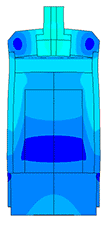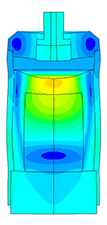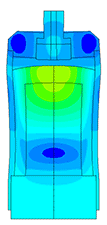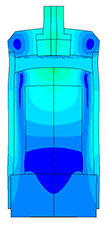
Плотномер
Определение паразитных колебаний у плотномера.
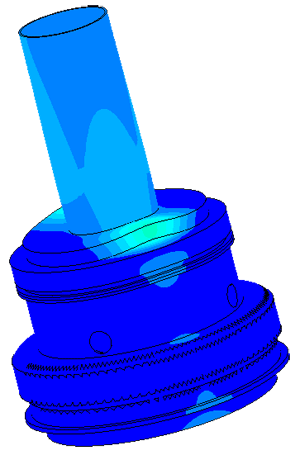

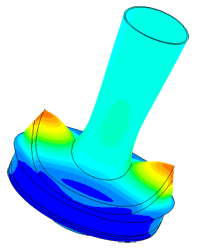
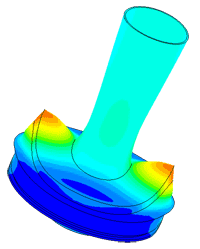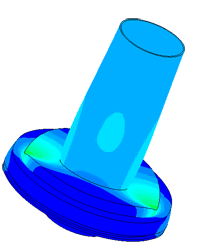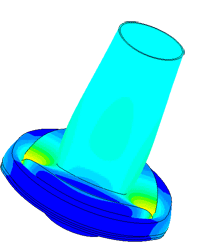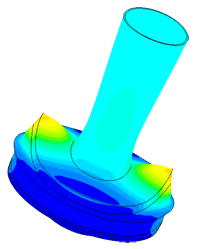
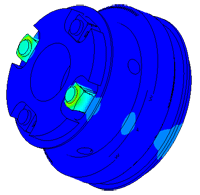
Модель пьезопакета, используемого в плотномере
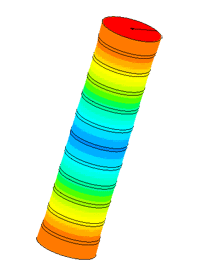
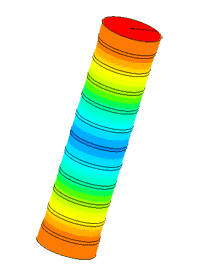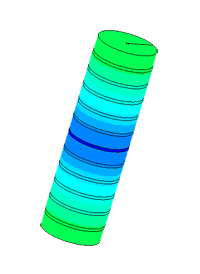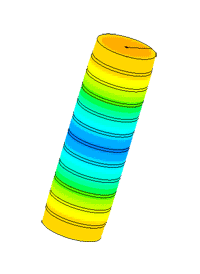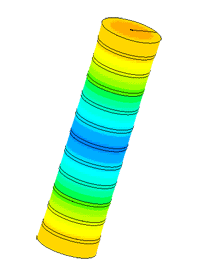
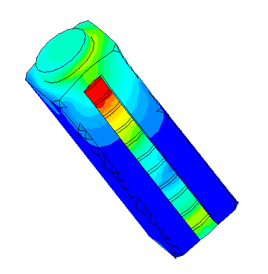
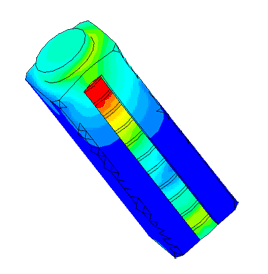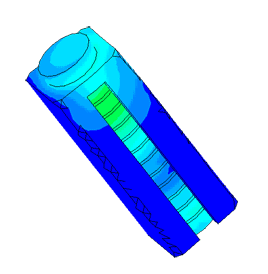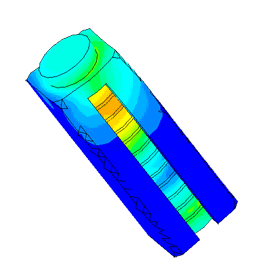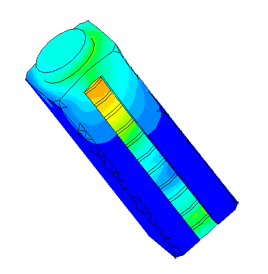
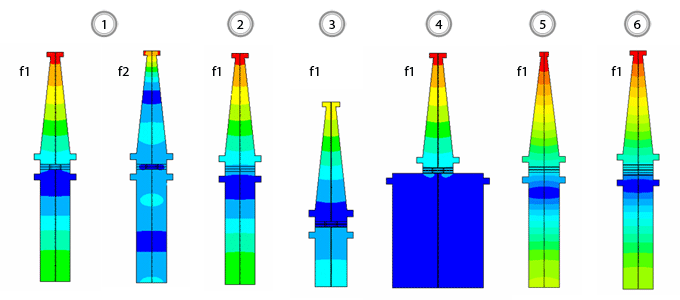
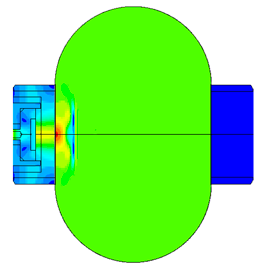
Диспергатор
| № | Модель | Частота 1 резонанса f1, Гц | Частота 2 резонанса f2, Гц | Механическая амплитуда колебаний кончика | |
| при f1, мкм | при f2, мкм | ||||
| 1 | первоначальная | 18971 | 45295 | 36,29 | 24,55 |
| 2 | с целым пьезоэлементом | 19318 | 46189 | 42,46 | 28,08 |
| 3 | с уменьшенной длинной груза | 24697 | 40213 | 38,37 | 36,65 |
| 4 | с увеличенным радиусом груза | 19226 | 39691 | 35,25 | 32,11 |
| 5 | с измененным концентратором | 20194 | 48475 | 40,33 | 37,03 |
| 6 | с 4 целыми пьезоэлементами | 18126 | 43230 | 46,85 | 33,94 |