Способы проектирования ультразвуковых преобразователей
- Преимущества моделирования датчиков
- Методы расчета ультразвуковых датчиков
- Расчет пьезоэлектрической среды методом конечных элементов
- Виды анализа
Преимущества моделирования датчиков
- Моделирование физических процессов позволяет:
- сэкономить средства на этапе разработки;
макетирование обычно очень дорого, а каждый следующий макет обычно существенно отличаются от предыдущего варианта; - лучше понять физику проблемы, позволяет вам посмотреть в "кишки" деталей;
внутренние амплитуды и механические напряжения трудно определить имперически; - проанализировать больше вариантов конструкций;
множество вариантов моделей может быть исследовано более быстро благодаря моделированию; - уменьшить число стадий создания прототипов;
моделирование дает множество ответов еще до начала создания прототипа; - выбрать оптимальную конструкцию датчика.
Примеры расчетов ультразвуковых датчиков Вы можете посмотреть в разделе 3D модели
Методы расчета ультразвуковых датчиков
При разработке ультразвуковых преобразователей, используются различные методы для расчета основных его характеристик. Часто используются следующие методы:
- создание эквивалентных электрических схем различной сложности, позволяющих рассчитать полосу частот преобразователя и размеры его составных частей;
- описание поведения излучателя с помощью теоретической модели плоский поршень, позволяет получить осциллограмму распределения давлений в жидкости [1];
- моделирование ультразвуковых преобразователей с помощью программных средств, основанных на методе конечных элементов, является наиболее комплексным методом, в полной мере позволяющим анализировать, разрабатывать и оптимизировать пьезоэлектрические датчики.
Для получения осциллограмм сигналов имеющих наибольшее совпадение с экспериментальными данными лучше всего подходят два последних метода.
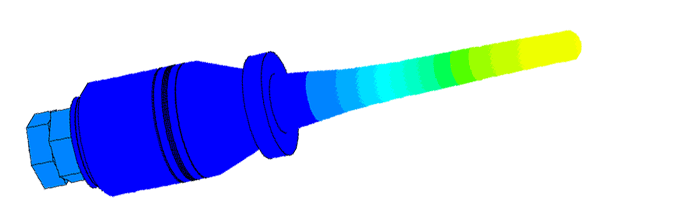
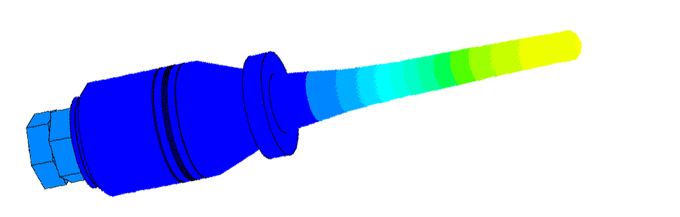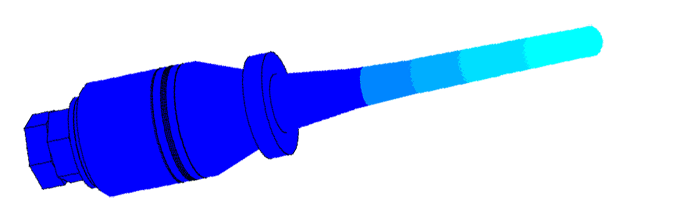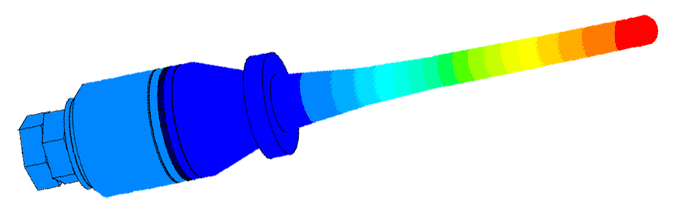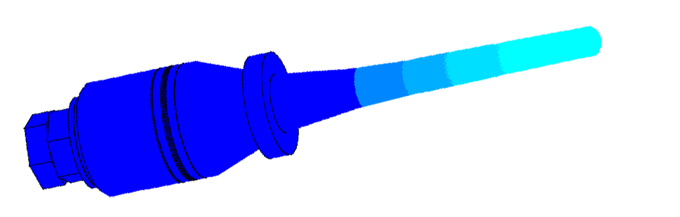
Масштаб колебаний 10000:1
Моды колебаний пьезоэлектрических преобразователей были проанализированы многими авторами из-за их важности в понимании поведения сигнала в преобразователе и в исследуемом образце. Хорошее понимание физики процесса распространения осциллограммы давления от цилиндрического преобразователя интерпретируется как суперпозиция хорошо известных плоских и краевых волн созданных пистоном [1]. Плоская волна распространяется в геометрическую область прямо вперед от источника, вместе с распространением краевых волн от периферии источника. Распределение давления пропорционально скорости частиц плоской волны, и краевой волны, излучаемой внутрь области в противофазе к плоской волне.
Согласно экспериментальным измерениям ультразвукового импульса в жидкости полученного многими авторами, измеренная краевая волна является искаженной по сравнению с моделью плоского поршня. Это говорит о том, что существуют другие эффекты, не предсказанные этой моделью. Неучтенным данной моделью важным эффектом является распространение поверхностных радиальных волн по керамике от ее границ. Эти радиальные волны создают коническую волну названную головной волной, которая распространяется в жидкости вместе с краевой волной. Это головная волна распространяется только перед краевой волной и интерферирует с ней. Характеристики головной волны зависят от свойств пьезокерамического материала, а так же от заднего слоя и корпуса преобразователя.
Проведенные сравнения модели плоского пистона с моделью созданной в коммерческой программе ANSYS, в частности в работе [2], показали, что анализ методом конечных элементов дает гораздо более близкие результаты к экспериментальным данным.
Таким образом метод конечных элементов является на данный момент самым точным среди всех и при этом охватывает все области, связанные с проектированием ультразвуковых преобразователей (пьезоэлектрический анализ, структурный анализ, акустический анализ и др.).
Расчет пьезоэлектрической среды методом конечных элементов
Метод конечных элементов [3] был впервые использован для анализа колебаний упругого материала примерно в 1950 году. Метод основан на вариационных методах, которые были использованы для анализа упругих материалов в 1940-х, для электромагнитного анализа в 1950-х и для пьезоэлектрических материалов в 1960-х.
Вариационные принципы для пьезоэлектрического вещества были сформулированы ЕрНисэ в 1967. ЕрНисэ использовал вариационные методы для анализа пьезоэлектрических дисков с различным соотношением диаметра и толщины. В то же самое время такие же вариационные принципы были получены Тирстеном из принципа Гамильтона. В дальнейшем метод конечных элементов широко использовался для решения задач связанных с пьезоэлектричеством.
Первые вычислительные примеры, применяющие метод конечных элементов для моделирования пьезоэлектрической среды были проведены Аликом, где собственные частоты пьезоэлектрического диска и структура керамики были приведены. В 1972 году Хунт, Смит и Барач проанализировали осесимметричный пьезоэлектрический сонар с помощью метода конечных элементов. Эта работа была позже расширена к случаю излучения пьезокерамики в акустическую среду.
В дальнейшие годы метод конечных элементов получил большую популярность для моделирования пьезоэлектрической среды, но действительно широкое использование метод получил после 1980 года. В 1986 году пьезоэлектрические элементы были включены в коммерческую программу, основанную на методе конечных элементов, ANSYS, которая использовалась многими группами для моделирования пьезоэлектрической среды. Позже такие элементы были включены в другие коммерческие доступные программы подобно ATILA, PZFlex, ABAQUS, MODULEF, PHOEBE, MSC и др.
Виды анализа
- Существуют следующие виды анализов:
- статический
- модальный
- гармонический
- анализ переходных процессов (динамический)
- спектральный
Модальный анализ
Модальный анализ помогает установить параметры колебаний конструкций: с его помощью определяются собственные частоты и формы колебаний. Кроме того, он используется как отправная точка для других, более подробных динамических расчетов, таких, как нестационарный динамический анализ или отклик системы на гармоническое воздействие.
В программе ANSYS модальный анализ является линейной процедурой. Любые нелинейности вроде пластичности или элементов зазора-контакта игнорируются, даже если они и заданы. Доступны четыре метода выявления собственных форм колебаний, в том числе и с учетом демпфирования.
Модальный анализ может проводиться для предварительно напряженных конструкций, таких, как лопатки вращающегося турбинного диска. Еще одной полезной особенностью является учет модальной циклической симметрии, что дает возможность свести анализ всей конструкции к анализу ее части.
Гармонический анализ
Любая достаточно длительная циклическая нагрузка вызывает гармонический отклик механической системы. Анализ реакции на гармоническое воздействие дает возможность определить установившийся отклик линейной механической системы на синусоидальную нагрузку и, таким образом, оценить способность системы противостоять резонансным явлениям, усталостному разрушению и другим вредным эффектам вибрации.
Основная идея метода состоит в том, чтобы получить отклик системы при нескольких частотах и построить зависимость определенных параметров (обычно перемещений) от частоты, затем выявить частоту, при которой реакция максимальна, и получить значения напряжений при этой частоте.
Любые нелинейности системы игнорируются. Анализ можно проводить для предварительно напряженной конструкции.
Анализ переходных процессов (динамический)
С появлением мощных и быстрых компьютеров, с большим объемом оперативной памяти, стало возможно выполнять анализ переходных процессов (transient analysis) пьезоэлектрических преобразователей.
Динамический анализ используется для определения реакции конструкции (в виде перемещений, деформаций, напряжений и усилий) на действие произвольной нагрузки, меняющейся во времени таким образом, что приходится учитывать инерционные эффекты и процессы рассеяния энергии.
Этот вид анализа гораздо более сложен, чем статический, поэтому, вообще говоря, необходимо предварять выполнение анализа работой по изучению физики проблемы, что может существенно сократить затраты инженерного труда и компьютерные ресурсы. Такая работа может состоять из следующих этапов:
- анализ более простых моделей (во многих случаях расчетные модели из пружин, масс и балок оказываются достаточными для получения динамического отклика сложной конструкции);
- проведение статического анализа перед введением нелинейностей (иногда можно убедиться, что в учете нелинейности нет необходимости);
- выполнение модального анализа для оценки реакции системы и определения шага решения по времени;
- использование метода подконструкций для линейных частей системы [4].
Спектральный анализ
Также некоторые инженеры используют моделирование во временной области с преобразованием Фурье, для того чтобы вычислить частотную характеристику.
Спектральный анализ – это решение задачи с использованием результатов модального анализа для расчета перемещений и напряжений в модели. Он в основном используется вместо временного анализа для определения реакции при случайных нагрузок или нагрузках, зависящих от времени, таких как землетрясение или ветровые нагрузки, нагрузки от морских волн, воздействие от реактивного двигателя, и т. д [5].
Спектр это график спектральной величины в функции от частоты, что определяет интенсивность и спектральный состав динамических нагрузок. Возможны три типа спектрального анализа:
- спектр реакции;
- метод динамического проектирования (DDAM);
- метод спектральной плотности мощности (PSD).
- Weight. J.P. Ultrasonic beam structures in fluid media, The Journal of the Acoustical Society of America, Vol.76, No. 4, 1984
- Jimmy E. San Miguel Medina Numerical modeling of a circular piezoelectric ultrasonic transducer radiating in water.: ABCM Symposium Series in Mechanics - Vol.2
- О.Зенкевич, К.Морган. Конечные элементы и аппроксимация.-Москва.: Мир, 1986.
- ANSYS User’s Manual for Revision 5.0
- Краткое руководство пользователя. Решение задач динамики в ANSYS.-Екатеринбург.:2002.